The Auckland Volcanic Field (AVF) is intraplate and active. GEONET seismic stations are used to monitor the field.
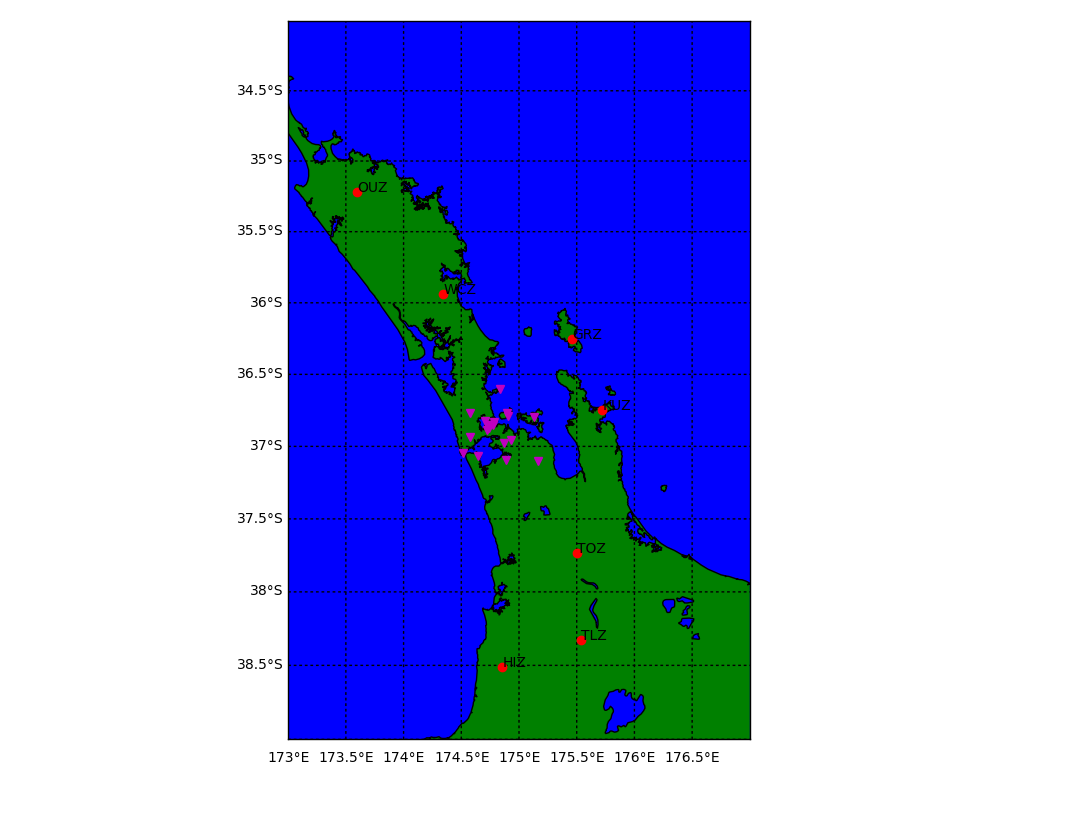
Stations distribution. Distinguished between those enclosing the AVF and those in the outer ring.
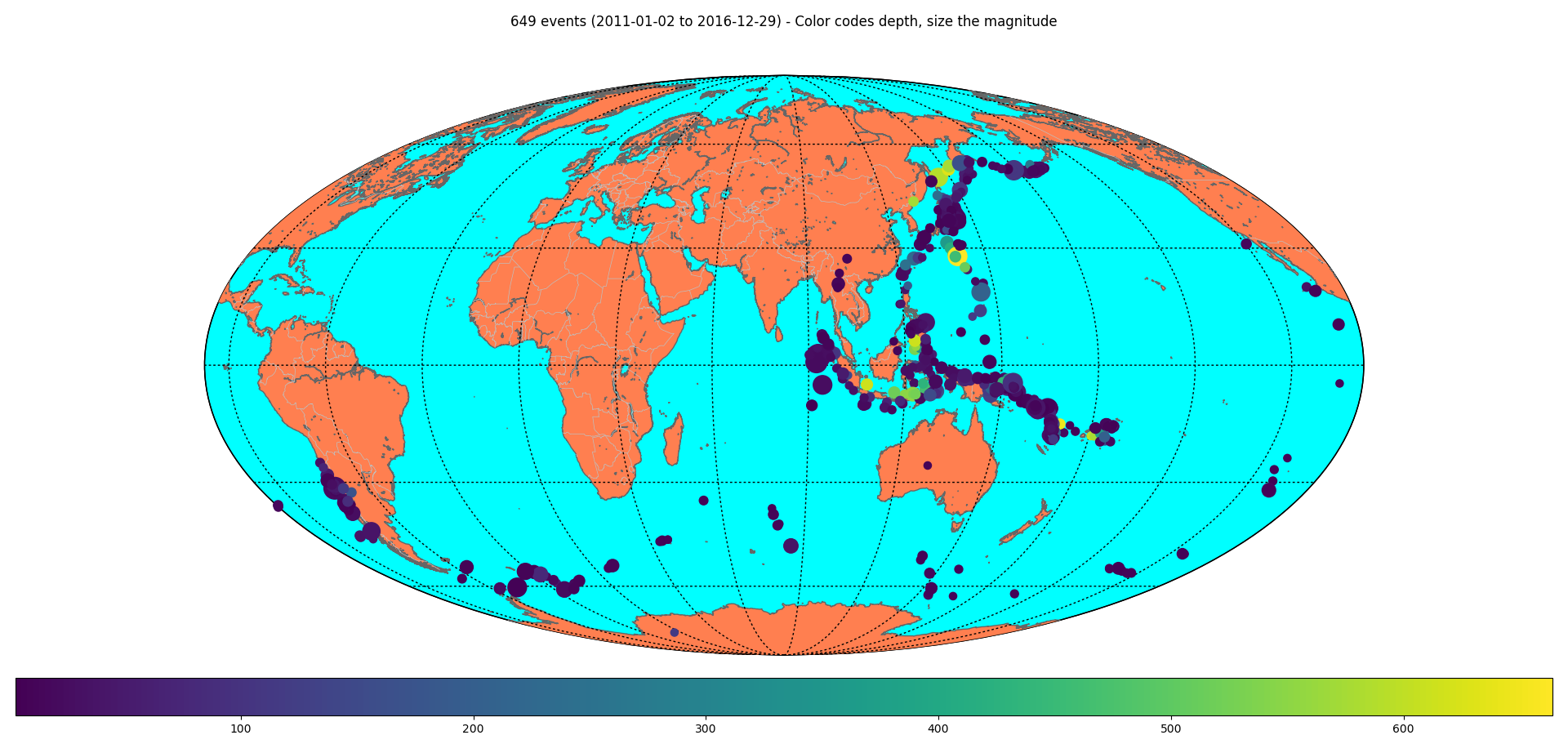
We propose to perform P- (and possibly S-) wave tomography to infer the structure beneath the AVF, with Nick Rawlinson’s FMTT. Our first test is to establish the resolution that we can expect from this exercise. Below, we plot the hypocentres of the earthquakes used in this test:
- Teleseismic sources
We compute synthetic seismic P-wave arrival times for the AVF seismic stations, as if the earth structure under the AVF has a checker-board pattern (see images on the left side of the gallery below). For this test, this will be our “true” model of the Earth. And so the objective of FMTT is to invert these synthetic travel times to recover the “true” model checker-board pattern. Areas where the inverted results show a checker-board pattern suggest a good resolution.
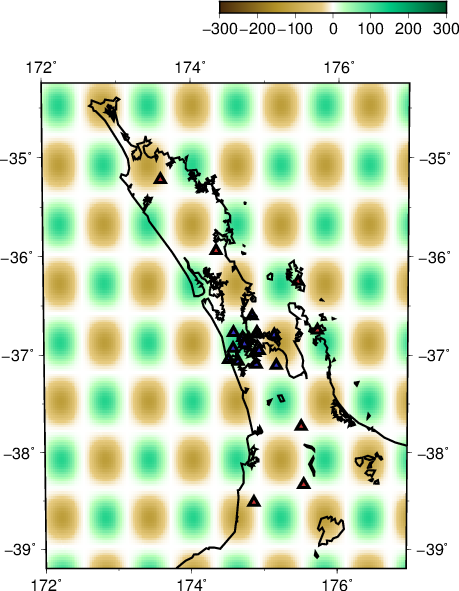
- Initial checker-board depth slice at 40 km
- Recovered checker-board P
- Recovered checker-board S
- Initial checker-board EW slice at -37.0
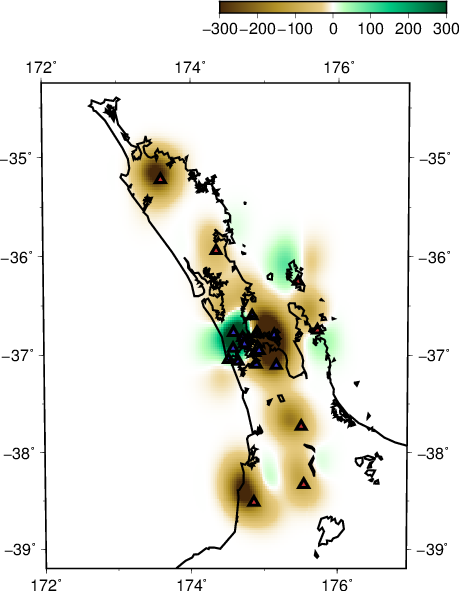
- Recovered checker-board P
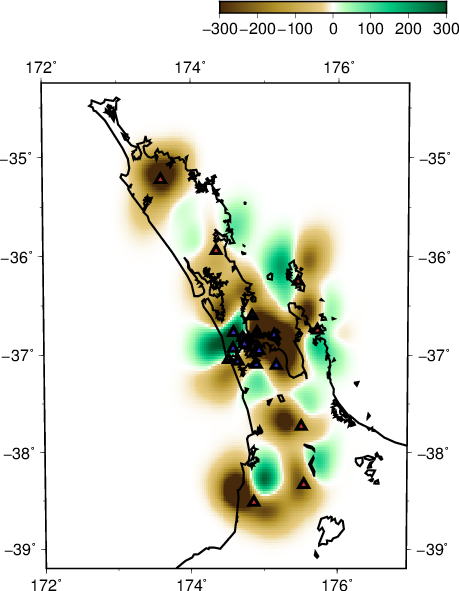
- Recovered checker-board S
- Initial checker-board NS slice at 174.75
- Recovered checker-board P
- Recovered checker-board S
Some of the sources need to be removed (17 out of 649 events) in order to run S wave tomography as the code could not determine the traveltimes of these 17 events from their respective sources to the base of the 3D model. Even still, S wave tomography shows a more prominent recovery overall. A major difference can be seen in the EW slice, where a band of positive anomaly cannot be recovered in the P wave equivalent.
Lateral resolution is better in NS rather than in EW orientation in particular at shallower depth. This is expected because the stations are more widely spread in this direction. In both though, resolution of the recovered checker-board is smeared, especially prominent in the lateral extent of the plot.
Directly below the AVF, we can see a pair of checker-board pattern being reflected. The EW slice at -37.0 shows this the best with minimal smearing. The pattern translates horizontally as well as shown in the depth slice. Also, some checker-board pattern persist even to the depth of >200 km.
Summary
- 50-km features seem to be resolved for the very shallow (20km?) and very deep (200km+) parts under the seismic array.
- S wave tomography shows a slighlty higher resolution, especially deeper and at greater lateral extent.
If we consider closer events we can obtain better resolution at shallower depth. In order to do this we use Nick Rawlinson’s FMTOMO, which results can be seen in this post.






Comments are closed.