The stations of the seismic network that monitors the Auckland Volcanic Field are a mix of surface and borehole seismographs. Our aim here is to figure out the orientation of the three orthogonal components of each seismometer.
The vertical component
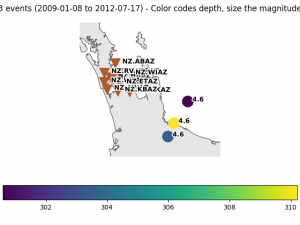
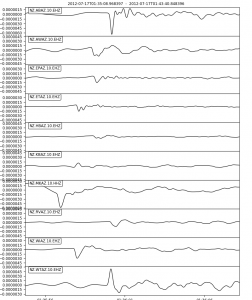
The vertical components of the seismic network are tested with some earthquakes with an epicentre that is only a ~100 km from the AVF. These are very deep earthquakes, assuring that high-frequency signal impinges from below on the network.
The figure below shows that seismic data from these events generally results in an arrival with a negative maximum, except stations KBAZ and WTAZ:
From this example and seismic data from other earthquakes, we conclude the polarity on the vertical component is reversed for stations KBAZ and WTAZ.
The horizontal components
The majority of the seismic stations in the AVF are in boreholes between 50 to 400 m deep. Particularly for these stations, the orientation of the horizontal components of the each station is unknown. Luckily, there are several techniques to estimate the orientations of the orthogonal horizontal components.
Ambient Noise Orientation
Stachnik et al. (2012) used a earthquake-sourced Rayleigh wave polarisation method to estimated the orientation of ocean bottom seismometers. Zha et al. (2013) used ambient seismic noise, applying a polarisation technique to the Rayleigh wave signal in CCFs to estimate the orientation of ocean-bottom-seismometers. Here we use ambient noise orientation, based on the method used by Zha et al. (2013), but we use it for borehole seismometers. We performed ambient noise orientation on all 3-component seismometers in the network, using the surface stations as a control group. The method involves three basic stages:
This method involves three stages:
- Computing the three-component cross-correlation functions for all station pairs from noise.
- Measurement of sensor orientation through an optimization process.
- Data selection and statistical analysis to obtain final orientation angles.
three-component cross-correlation functions
Cross-correlation functions (CCFs) can be computed for any pairs of seismic sensors. Computing all the possible cross-correlation functions for a pair of three-component seismometers would produce nine functions. For this technique, we use some of the CCFs that potentially contain Rayleigh wave signal. Rayleigh wave motion occurs in the vertical plane so we expect virtual Rayleigh wave signal to emerge in the vertical-vertical(C_zz), and the radial-vertical (C_rz) CCFs. For seismometers with unknown orientation, the C_rz data is distributed across the horizontal-verticals (C_1z and C_2z) cross-correlation functions.
Optimisation
For each pair of seismometers, the symmetric CCFs are bandpass filtered to the frequency band where Rayleigh wave with the greatest amplitude are expected to emerge (In our case 0.05–0.5Hz). We then perform a grid-search through 360-degrees, each performing as an estimate of the angle that would rotate C_1z and C_2z into the C_rz and C_tz . For each estimate of C_rz, the zero-lag cross-correlation and coherence between the C_rz and 90-degrees phase-shifted C_zz is computed. The maximum cross-correlation marks the best estimate of C_rz. The coherence at maximum cross-correlation is used in the data selection. The back azimuth can then be calculated because the coordinates of both stations are known.
The figure below this process is illustrated for the AWAZ-ABAZ pair. On the left, there is C_zz, C_1z, and C_2z, and the phase shifted C_zz in the dashed red. In the middle panel , the correlation and coherence are plotted by angle. On the right, there is C_zz, and the C_rz, and C_tz based on the angle at maximum correlation (260 degrees in this case), and the phase shifted C_zz in the dashed red.
Data Selection and Statistical Analysis
Estimates with a coherence below 0.5 at maximum correlation tend to be scattered to a greater degree. These coherences were discarded. We then take the mean of the remaining estimates as our final estimate of the orientation. In the figure below, the estimates for the AWAZ station are presented in a polar plot. The radial axis represents the number of estimates in each 1-degree bin. Red represents estimates with coherences below 0.5 that are removed.
Stachnik, J.C., Sheehan, A.F., Zietlow, D.W., Yang, Z., Collins, J., & Ferris, A., 2012. Determination of New Zealand ocean bottom seismometer orientation via Rayleigh-wave polarization. Seismological Research Letters, 83(4).
Zha Y, Webb SC, & Menke W. Determining the orientations of ocean bottom seismometers using ambient noise correlation. Geophysical Research Letters. 2013 Jul 28;40(14).
Comments are closed.